Wavelets

Note

Go to the end to download the full example code.

Wavelets#

Wavelet Analysis is a mathematical tool that decomposes signals or data into different frequency components, allowing localized analysis in both time and frequency domains. Unlike Fourier analysis, which provides only global frequency information, wavelets use scalable and shiftable basis functions (“wavelets”) to capture transient features, trends, and discontinuities at multiple resolutions.

  • Extreme Event Detection: Identifies localized phenomena (e.g., hurricanes, heavy rainfall) by isolating abrupt changes in atmospheric data.

  • Climate Variability Studies: Analyzes multi-scale oscillations (e.g., El Niño, Madden-Julian Oscillation) and their time-frequency characteristics.

  • Turbulence & Boundary Layer Processes: Resolves eddy structures and energy cascades in high-resolution wind/temperature data.

  • Data Denoising: Separates meaningful signals from noise in observational datasets (e.g., satellite measurements).

  • Spatio-Temporal Patterns: Examines non-stationary relationships, such as teleconnections between distant climate variables.

Wavelets are particularly valuable for non-stationary meteorological data, where traditional spectral methods fall short.

See also

  • Torrence, C., & Compo, G. P. (1998). A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, 79(1), 61-78. https://doi.org/10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2

  • Torrence, C., & Webster, P. J. (1999). Interdecadal Changes in the ENSO–Monsoon System. Journal of Climate, 12(8), 2679-2690. https://doi.org/10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2

  • Grinsted, A., Moore, J. C., and Jevrejeva, S.: Application of the cross wavelet transform and wavelet coherence to geophysical time series, Nonlin. Processes Geophys., 11, 561–566, https://doi.org/10.5194/npg-11-561-2004, 2004.

Before proceeding with all the steps, first import some necessary libraries and packages

import xarray as xr
import matplotlib.pyplot as plt
import easyclimate as ecl

Import the required nino3 data and perform wavelet analysis

Tip

You can download following datasets here: Download test_input_nino3_wavelet.nc

data_nino3 = xr.open_dataset('test_input_nino3_wavelet.nc')['nino3']
result_data = ecl.filter.calc_timeseries_wavelet_transform(data_nino3, dt = 0.25)
result_data

Allen and Smith AR(1) model estimate of the lag-one autocorrelation: lag1 =  0.7673996830077151

<xarray.Dataset> Size: 247kB
Dimensions:        (period: 29, time: 504)
Coordinates:
  * period         (period) float64 232B 0.5165 0.6143 0.7305 ... 55.6 66.11
  * time           (time) datetime64[ns] 4kB 1871-01-31 ... 1996-10-31
Data variables:
    power          (period, time) float64 117kB 0.008459 0.0105 ... 1.193 1.191
    sig            (period, time) float64 117kB 0.03977 0.04934 ... 0.09796
    global_ws      (period) float64 232B 0.02912 0.04269 ... 0.5386 0.7283
    global_signif  (period) float64 232B 0.08257 0.09085 0.1088 ... 10.92 11.26
    coi            (time) float64 4kB 0.0 0.0 0.1826 0.3652 ... 0.1826 0.0 0.0
    coi_bottom     (time) float64 4kB 66.11 66.11 66.11 ... 66.11 66.11 66.11
Attributes:
    dt:                  0.25
    scale:               [ 0.5         0.59460356  0.70710678  0.84089642  1....
    sigtest_global:      time-average test
    sigtest_wavelet:     regular chi-square test
    lag1:                0.7673996830077151
    dof:                 [503.5        503.40539644 503.29289322 503.15910358...
    mother:              morlet
    significance_level:  0.95


Plotting the global wavelet spectrum

fig, ax = plt.subplots()
ecl.filter.draw_global_wavelet_spectrum(result_data, ax = ax)
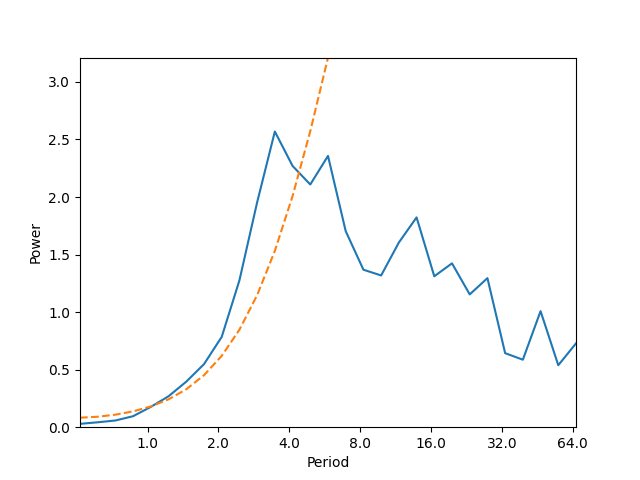
plot wavelet

And plotting the wavelet transform

fig, ax = plt.subplots()
ecl.filter.draw_wavelet_transform(result_data, ax = ax)
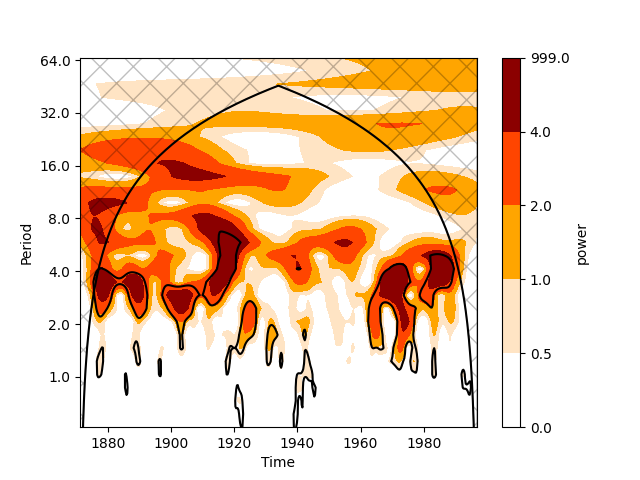
plot wavelet

Total running time of the script: (0 minutes 3.433 seconds)