2D Spatial Parabolic Cylinder Function

Note

Go to the end to download the full example code.

2D Spatial Parabolic Cylinder Function#

Ever wondered how atmospheric waves boogie along the equator? Let’s explore how to isolate these fascinating dancers (Kelvin waves, Rossby waves, and friends) using parabolic cylinder functions!

Before proceeding with all the steps, first import some necessary libraries and packages

import xarray as xr
import cartopy.crs as ccrs
import easyclimate as ecl

Loading the Data#

First, we need some atmospheric data to work with - think of this as setting up the dance floor for our waves:

Tip

You can download following datasets here: Download uwnd_vwnd_hgt_equtorial_2021_2024.nc

uvz_data = xr.open_dataset("uwnd_vwnd_hgt_equtorial_2021_2024.nc")
uvz_data

<xarray.Dataset> Size: 43MB
Dimensions:  (time: 1461, lon: 144, lat: 17)
Coordinates:
  * time     (time) datetime64[ns] 12kB 2021-01-01 2021-01-02 ... 2024-12-31
  * lon      (lon) float32 576B 0.0 2.5 5.0 7.5 10.0 ... 350.0 352.5 355.0 357.5
  * lat      (lat) float32 68B -20.0 -17.5 -15.0 -12.5 ... 12.5 15.0 17.5 20.0
    level    float32 4B ...
Data variables:
    hgt      (time, lat, lon) float32 14MB ...
    uwnd     (time, lat, lon) float32 14MB ...
    vwnd     (time, lat, lon) float32 14MB ...


Isolating Wave Types#

Now for the star of our show: the 2D spatial parabolic cylinder function filter easyclimate.filter.filter_2D_spatial_parabolic_cylinder_function! This function works like a talented bouncer, only letting specific wave types into our analysis:

result = ecl.filter.filter_2D_spatial_parabolic_cylinder_function(uvz_data.uwnd, uvz_data.vwnd, uvz_data.hgt)
result

<xarray.Dataset> Size: 343MB
Dimensions:    (wave_type: 4, lat: 17, lon: 144, time: 1461)
Coordinates:
  * wave_type  (wave_type) <U6 96B 'kelvin' 'wmrg' 'r1' 'r2'
  * lat        (lat) float32 68B -20.0 -17.5 -15.0 -12.5 ... 12.5 15.0 17.5 20.0
    level      float32 4B 850.0
  * lon        (lon) float32 576B 0.0 2.5 5.0 7.5 ... 350.0 352.5 355.0 357.5
  * time       (time) datetime64[ns] 12kB 2021-01-01 2021-01-02 ... 2024-12-31
Data variables:
    u          (wave_type, time, lat, lon) float64 114MB -0.001955 ... 0.0107
    v          (wave_type, time, lat, lon) float64 114MB 0.0 0.0 ... 0.01983
    z          (wave_type, time, lat, lon) float64 114MB -0.004085 ... 0.0642


Visualizing the Waves#

Let’s meet our wave dancers one by one and see their unique moves!

The Graceful Kelvin Wave#

Kelvin waves move eastward with elegant symmetry, like ballet dancers:

fig, ax = ecl.plot.quick_draw_spatial_basemap(figsize=(9, 4), central_longitude=180)
ax.set_extent([20, 180, -20, 20], crs = ccrs.PlateCarree())

# Contour plot for height field
result.sel(wave_type = "kelvin").z.sel(time = "2023-12-15").plot.contourf(
    ax = ax,
    levels=21,
    transform = ccrs.PlateCarree(),
    cbar_kwargs={"location": "bottom", "aspect": 50, "shrink": 0.5},
)

# Quiver plot for wind vectors
result.sel(wave_type = "kelvin")[["u", "v"]].sel(time = "2023-12-15").thin(lon=1, lat=1).plot.quiver(
    x = "lon", y = 'lat',
    u = "u", v = "v",
    ax = ax,
    scale = 30,
    headlength = 5,
    minlength = 1.5,
    transform = ccrs.PlateCarree()
)

ax.set_title("Kelvin Waves")
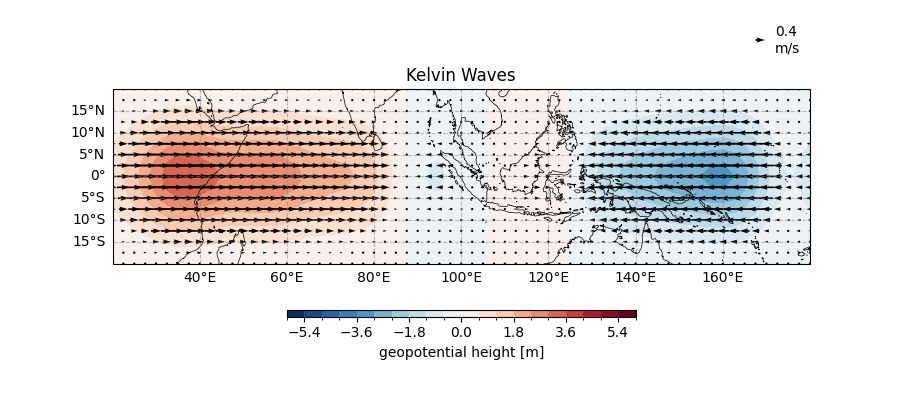
Kelvin Waves
Text(0.5, 1.0, 'Kelvin Waves')

The WMRG Wave#

Westward-moving Mixed Rossby-Gravity waves have more complex moves, like contemporary dancers:

fig, ax = ecl.plot.quick_draw_spatial_basemap(figsize=(9, 4), central_longitude=180)
ax.set_extent([20, 180, -20, 20], crs = ccrs.PlateCarree())

result.sel(wave_type = "wmrg").z.sel(time = "2023-12-15").plot.contourf(
    ax = ax,
    levels=21,
    transform = ccrs.PlateCarree(),
    cbar_kwargs={"location": "bottom", "aspect": 50, "shrink": 0.5},
)
result.sel(wave_type = "wmrg")[["u", "v"]].sel(time = "2023-12-15").thin(lon=1, lat=1).plot.quiver(
    x = "lon", y = 'lat',
    u = "u", v = "v",
    ax = ax,
    scale = 30,
    headlength = 5,
    minlength = 1.5,
    transform = ccrs.PlateCarree()
)

ax.set_title("Westward Mixed Rossby-Gravity Waves")
Westward Mixed Rossby-Gravity Waves
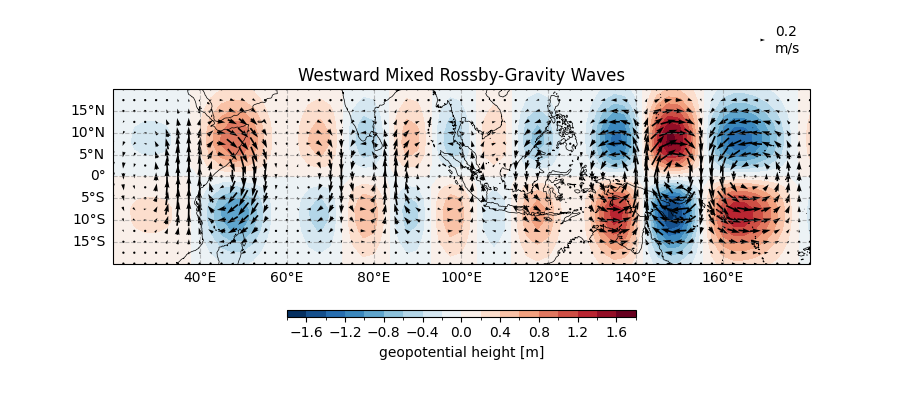
Text(0.5, 1.0, 'Westward Mixed Rossby-Gravity Waves')

The Rossby Waves#

Rossby waves come in different “generations”, let’s meet the first two:

\([n=1]\) Rossby Wave#

fig, ax = ecl.plot.quick_draw_spatial_basemap(figsize=(9, 4), central_longitude=180)
ax.set_extent([20, 180, -20, 20], crs = ccrs.PlateCarree())

result.sel(wave_type = "r1").z.sel(time = "2023-12-15").plot.contourf(
    ax = ax,
    levels=21,
    transform = ccrs.PlateCarree(),
    cbar_kwargs={"location": "bottom", "aspect": 50, "shrink": 0.5},
)
result.sel(wave_type = "r1")[["u", "v"]].sel(time = "2023-12-15").thin(lon=1, lat=1).plot.quiver(
    x = "lon", y = 'lat',
    u = "u", v = "v",
    ax = ax,
    scale = 70,
    headlength = 5,
    minlength = 1.5,
    transform = ccrs.PlateCarree()
)

ax.set_title("$n = 1$ Equatorial Rossby Waves")
$n = 1$ Equatorial Rossby Waves
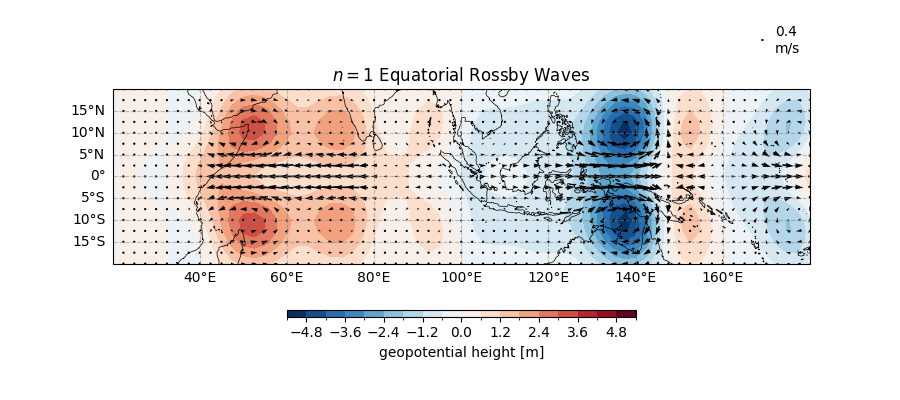
Text(0.5, 1.0, '$n = 1$ Equatorial Rossby Waves')

\([n=2]\) Rossby Wave#

fig, ax = ecl.plot.quick_draw_spatial_basemap(figsize=(9, 4), central_longitude=180)
ax.set_extent([20, 180, -20, 20], crs = ccrs.PlateCarree())

result.sel(wave_type = "r2").z.sel(time = "2023-12-15").plot.contourf(
    ax = ax,
    levels=21,
    transform = ccrs.PlateCarree(),
    cbar_kwargs={"location": "bottom", "aspect": 50, "shrink": 0.5},
)
result.sel(wave_type = "r2")[["u", "v"]].sel(time = "2023-12-15").thin(lon=1, lat=1).plot.quiver(
    x = "lon", y = 'lat',
    u = "u", v = "v",
    ax = ax,
    scale = 40,
    headlength = 5,
    minlength = 1.5,
    transform = ccrs.PlateCarree()
)

ax.set_title("$n = 2$ Equatorial Rossby Waves")
$n = 2$ Equatorial Rossby Waves
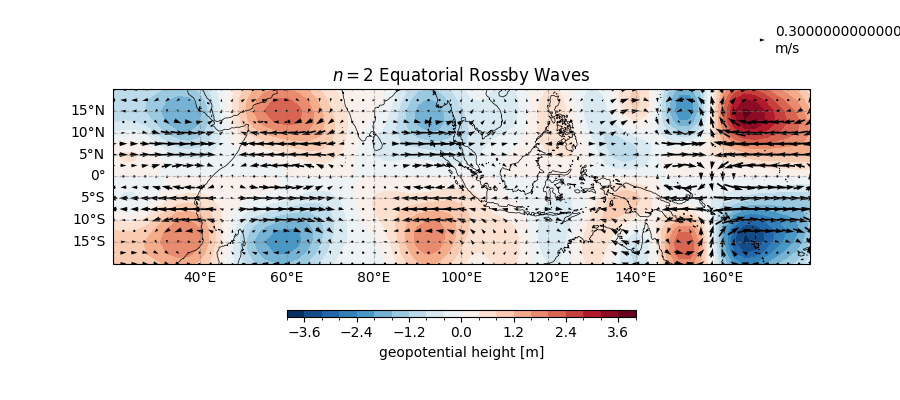
Text(0.5, 1.0, '$n = 2$ Equatorial Rossby Waves')

Behind the Scenes: How the Magic Works#

The easyclimate.filter.filter_2D_spatial_parabolic_cylinder_function performs some serious atmospheric wizardry:

  1. Detrending and Windowing: Prepares the data by removing trends and applying spectral windows

  2. Variable Transformation: Creates new variables that better represent wave structures

  3. Fourier Analysis: Identifies frequency and wavenumber components

  4. Projection: Maps the data onto parabolic cylinder functions that match equatorial wave structures

  5. Filtering: Isolates specific wave types based on their characteristic patterns

  6. Reconstruction: Brings everything back to physical space for visualization

Each wave type has its own signature moves:

  • Kelvin Waves: Eastward-moving, symmetric about the equator (\(n=0\) mode)

  • WMRG Waves: Westward-moving with mixed characteristics (\(n=1\) mode)

  • Rossby Waves: Westward-moving with more complex structures (\(n=2\), \(n=3\) modes)

Total running time of the script: (0 minutes 9.332 seconds)

Contents