Empirical Orthogonal Function (EOF) and Maximum Covariance Analysis (MCA)

Note

Go to the end to download the full example code.

Empirical Orthogonal Function (EOF) and Maximum Covariance Analysis (MCA)#

Before proceeding with all the steps, first import some necessary libraries and packages

import xarray as xr
import easyclimate as ecl
import matplotlib.pyplot as plt
import cartopy.crs as ccrs

Empirical Orthogonal Function#

Read raw precipitation and temperature data

t_data = xr.open_dataset("t_ERA5_1982-2022_N80.nc").t.sel(time = slice("1982-01-01", "2020-12-31")).sortby("lat")
precip_data = xr.open_dataset("precip_ERA5_1982-2020_N80.nc").precip.sel(time = slice("1982-01-01", "2020-12-31")).sortby("lat")

Tip

You can download following datasets here:

Be limited to the East Asia region and conduct empirical orthogonal function (EOF) analysis on it

precip_data_EA = precip_data.sel(lon = slice(105, 130), lat = slice(20, 40))
model = ecl.eof.get_EOF_model(precip_data_EA, lat_dim = 'lat', lon_dim = 'lon', remove_seasonal_cycle_mean = True, use_coslat = True)
eof_analysis_result = ecl.eof.calc_EOF_analysis(model)
eof_analysis_result.to_netcdf("eof_analysis_result.nc")

Load the analyzed data

eof_analysis_result = xr.open_dataset("eof_analysis_result.nc")
eof_analysis_result

<xarray.Dataset> Size: 77kB
Dimensions:                   (mode: 10, lat: 18, lon: 22, time: 468)
Coordinates:
  * mode                      (mode) int64 80B 1 2 3 4 5 6 7 8 9 10
  * lat                       (lat) float64 144B 20.75 21.87 ... 38.69 39.81
  * lon                       (lon) float64 176B 105.8 106.9 ... 128.2 129.4
  * time                      (time) datetime64[ns] 4kB 1982-01-31T18:00:00 ....
    month                     (time) int64 4kB ...
Data variables:
    EOF                       (mode, lat, lon) float64 32kB ...
    PC                        (mode, time) float64 37kB ...
    explained_variance        (mode) float64 80B ...
    explained_variance_ratio  (mode) float64 80B ...
    singular_values           (mode) float64 80B ...


Draw the leading first and second modes

fig = plt.figure(figsize = (12, 8))
fig.subplots_adjust(hspace = 0.15, wspace = 0.2)
gs = fig.add_gridspec(3, 2)

proj = ccrs.PlateCarree(central_longitude = 200)
proj_trans = ccrs.PlateCarree()

axi = fig.add_subplot(gs[0:2, 0], projection = proj)
draw_data = eof_analysis_result["EOF"].sel(mode = 1)
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")

axi = fig.add_subplot(gs[2, 0])
ecl.plot.line_plot_with_threshold(eof_analysis_result["PC"].sel(mode = 1), line_plot=False)
axi.set_ylim(-0.2, 0.2)

axi = fig.add_subplot(gs[0:2, 1], projection = proj)
draw_data = eof_analysis_result["EOF"].sel(mode = 2)
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")

axi = fig.add_subplot(gs[2, 1])
ecl.plot.line_plot_with_threshold(eof_analysis_result["PC"].sel(mode = 2), line_plot=False)
axi.set_ylim(-0.2, 0.2)
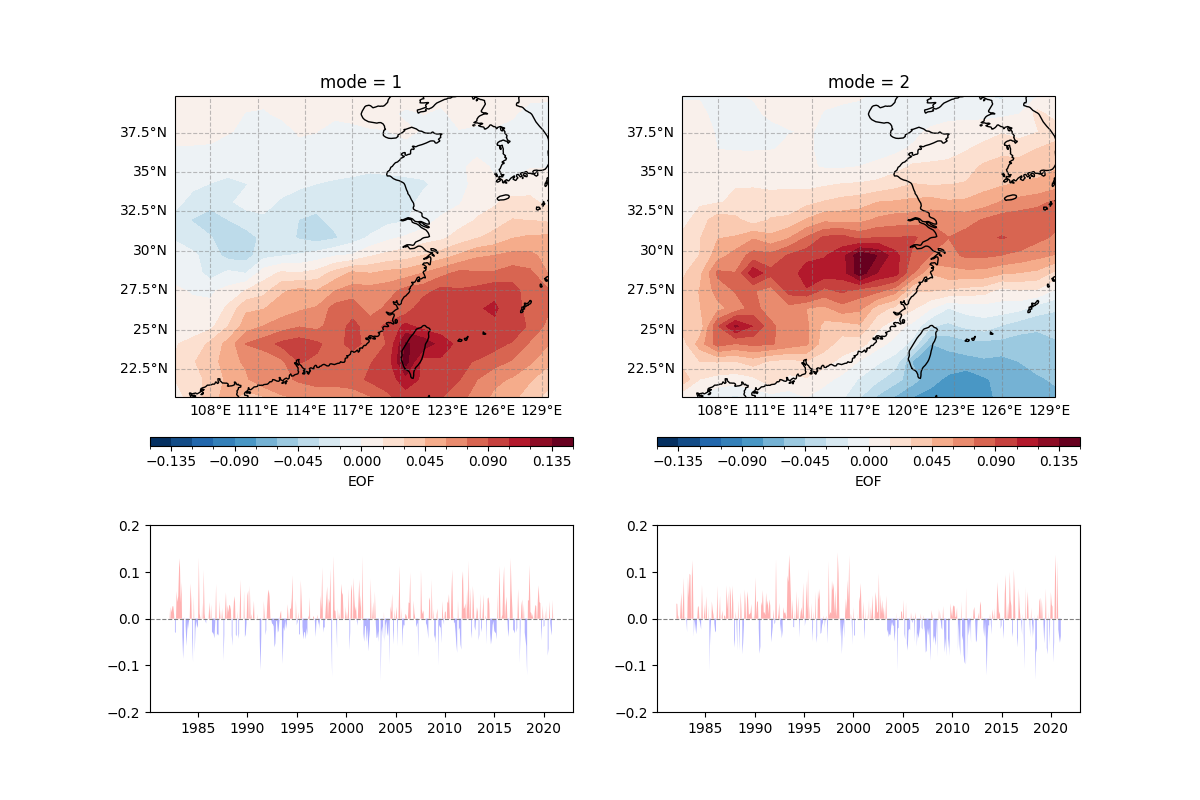
mode = 1, mode = 2
(-0.2, 0.2)

Rotated Empirical Orthogonal Function#

Here, we conduct rotated empirical orthogonal function (REOF) analysis on it

model = ecl.eof.get_REOF_model(precip_data_EA, lat_dim = 'lat', lon_dim = 'lon', remove_seasonal_cycle_mean = True, use_coslat = True)
reof_analysis_result = ecl.eof.calc_REOF_analysis(model)
reof_analysis_result.to_netcdf("reof_analysis_result.nc")

Now load the data

reof_analysis_result = xr.open_dataset("reof_analysis_result.nc")
reof_analysis_result

<xarray.Dataset> Size: 22kB
Dimensions:                   (mode: 2, lat: 18, lon: 22, time: 468)
Coordinates:
  * mode                      (mode) int64 16B 1 2
  * lat                       (lat) float64 144B 20.75 21.87 ... 38.69 39.81
  * lon                       (lon) float64 176B 105.8 106.9 ... 128.2 129.4
  * time                      (time) datetime64[ns] 4kB 1982-01-31T18:00:00 ....
    month                     (time) int64 4kB ...
Data variables:
    EOF                       (mode, lat, lon) float64 6kB ...
    PC                        (mode, time) float64 7kB ...
    explained_variance        (mode) float64 16B ...
    explained_variance_ratio  (mode) float64 16B ...
    singular_values           (mode) float64 16B ...


fig = plt.figure(figsize = (12, 8))
fig.subplots_adjust(hspace = 0.15, wspace = 0.2)
gs = fig.add_gridspec(3, 2)

proj = ccrs.PlateCarree(central_longitude = 200)
proj_trans = ccrs.PlateCarree()

axi = fig.add_subplot(gs[0:2, 0], projection = proj)
draw_data = reof_analysis_result["EOF"].sel(mode = 1)
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")

axi = fig.add_subplot(gs[2, 0])
ecl.plot.line_plot_with_threshold(reof_analysis_result["PC"].sel(mode = 1), line_plot=False)
axi.set_ylim(-0.2, 0.2)

axi = fig.add_subplot(gs[0:2, 1], projection = proj)
draw_data = reof_analysis_result["EOF"].sel(mode = 2)
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")

axi = fig.add_subplot(gs[2, 1])
ecl.plot.line_plot_with_threshold(reof_analysis_result["PC"].sel(mode = 2), line_plot=False)
axi.set_ylim(-0.2, 0.2)
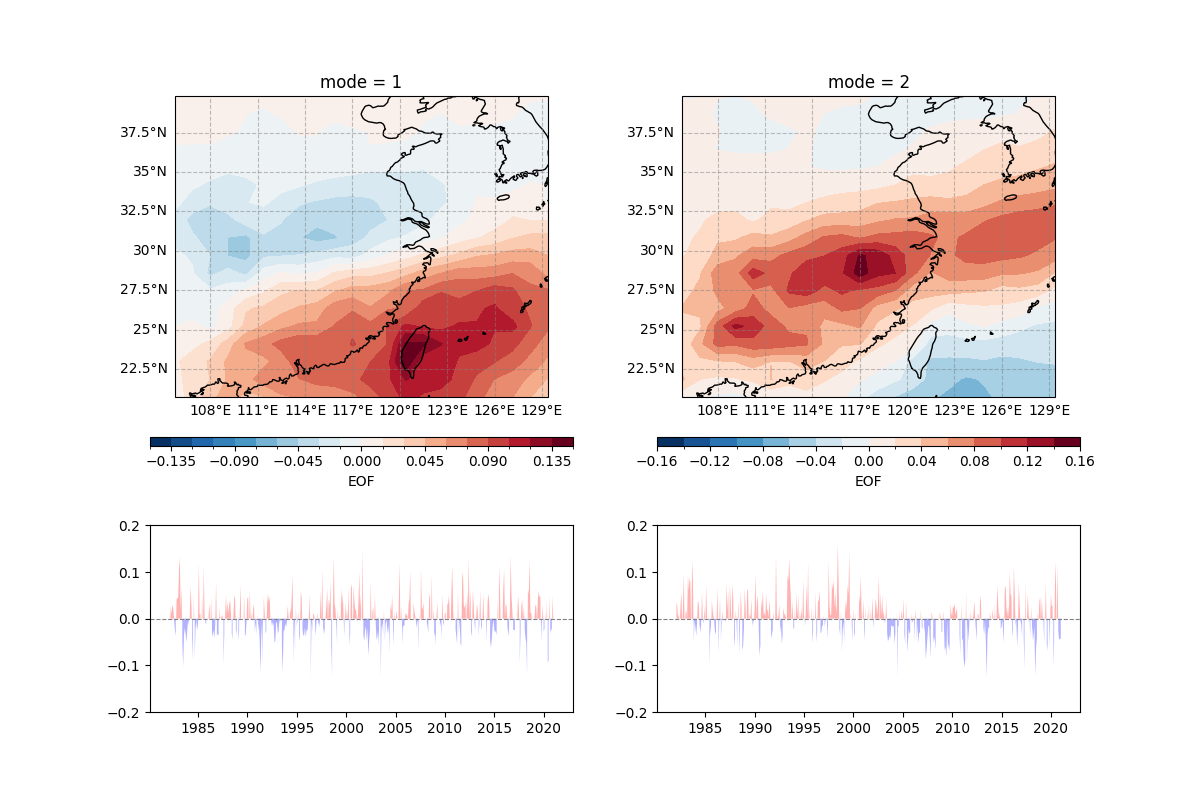
mode = 1, mode = 2
(-0.2, 0.2)

Maximum Covariance Analysis#

Be limited to the East Asia region for precipitation and temperature.

precip_data_EA = precip_data.sel(lon = slice(105, 130), lat = slice(20, 40))
t_data_EA = t_data.sel(lon = slice(105, 130), lat = slice(20, 40)).sel(level = 1000)

Maximum Covariance Analysis (MCA) between two data sets.

mca_model = ecl.eof.get_MCA_model(precip_data_EA, t_data_EA, lat_dim="lat", lon_dim="lon", n_modes=2, use_coslat=True,random_state=0)
mca_analysis_result = ecl.eof.calc_MCA_analysis(mca_model)
mca_analysis_result.to_zarr("mca_analysis_result.zarr")

Now load the data

mca_analysis_result = ecl.open_datanode("./mca_analysis_result.zarr")
mca_analysis_result
easyclimate.DataNode
'root'
▶root
▶EOF
▶PC
▶correlation_coefficients_X:xarray.Dataset
▶correlation_coefficients_Y:xarray.Dataset
▶covariance_fraction:xarray.Dataset
▶cross_correlation_coefficients:xarray.Dataset
▶fraction_variance_X_explained_by_X:xarray.Dataset
▶fraction_variance_Y_explained_by_X:xarray.Dataset
▶fraction_variance_Y_explained_by_Y:xarray.Dataset
▶heterogeneous_patterns
▶homogeneous_patterns
▶squared_covariance_fraction:xarray.Dataset


Draw results for leading modes

fig = plt.figure(figsize = (9, 6))
fig.subplots_adjust(hspace = 0.15, wspace = 0.1)
gs = fig.add_gridspec(3, 2)

proj = ccrs.PlateCarree(central_longitude = 200)
proj_trans = ccrs.PlateCarree()

# ---------------
axi = fig.add_subplot(gs[0:2, 0], projection = proj)
draw_data = mca_analysis_result["EOF/left_EOF"].sel(mode = 2).left_EOF
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('left EOF2')

# ---------------
axi = fig.add_subplot(gs[2, 0])
ecl.plot.line_plot_with_threshold(mca_analysis_result["PC/left_PC"].sel(mode = 1).left_PC, line_plot=False)
axi.set_ylim(-0.04, 0.04)

# ---------------
axi = fig.add_subplot(gs[0:2, 1], projection = proj)
draw_data = mca_analysis_result["EOF/right_EOF"].sel(mode = 2).right_EOF
draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('right EOF2')

# ---------------
axi = fig.add_subplot(gs[2, 1])
ecl.plot.line_plot_with_threshold(mca_analysis_result["PC/right_PC"].sel(mode = 1).right_PC, line_plot=False)
axi.set_ylim(-0.04, 0.04)
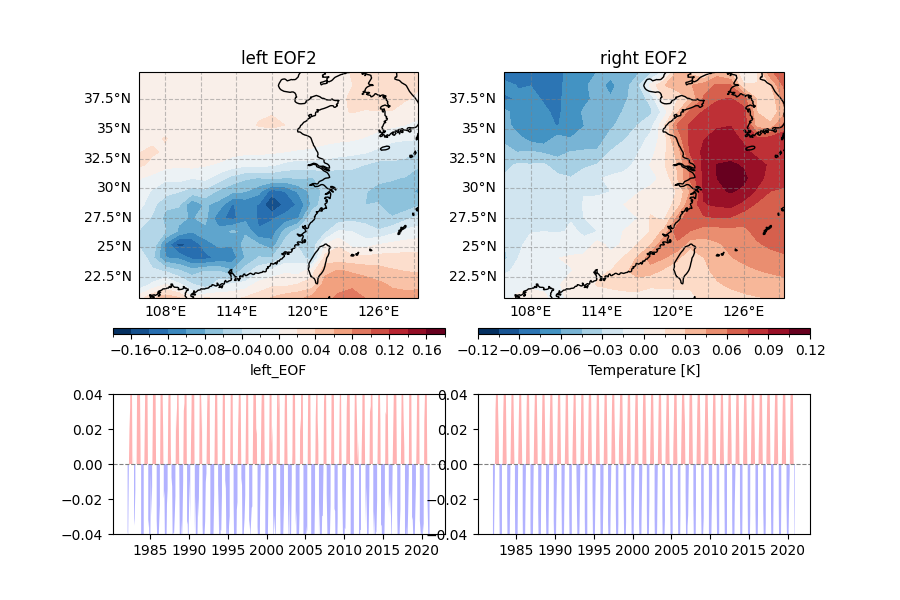
left EOF2, right EOF2
(-0.04, 0.04)

Draw the figures for both homogeneous and heterogeneous patterns

proj = ccrs.PlateCarree(central_longitude = 200)
proj_trans = ccrs.PlateCarree()

fig, ax = plt.subplots(2, 2, figsize = (9, 8), subplot_kw={"projection": proj})

# ---------------
axi = ax[0, 0]

draw_data = mca_analysis_result["heterogeneous_patterns/left_heterogeneous_patterns"].sel(mode = 2).left_heterogeneous_patterns
p_data = mca_analysis_result["heterogeneous_patterns/pvalues_of_left_heterogeneous_patterns"].sel(mode = 2).pvalues_of_left_heterogeneous_patterns

draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
ecl.plot.draw_significant_area_contourf(p_data, ax = axi, thresh=0.1, transform=proj_trans)

axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('Left Heterogeneous Patterns')

# ---------------
axi = ax[0, 1]

draw_data = mca_analysis_result["heterogeneous_patterns/right_heterogeneous_patterns"].sel(mode = 2).right_heterogeneous_patterns
p_data = mca_analysis_result["heterogeneous_patterns/pvalues_of_right_heterogeneous_patterns"].sel(mode = 2).pvalues_of_right_heterogeneous_patterns

draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
ecl.plot.draw_significant_area_contourf(p_data, ax = axi, thresh=0.1, transform=proj_trans)

axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('Right Heterogeneous Patterns')

# ---------------
axi = ax[1, 0]

draw_data = mca_analysis_result["homogeneous_patterns/left_homogeneous_patterns"].sel(mode = 2).left_homogeneous_patterns
p_data = mca_analysis_result["homogeneous_patterns/pvalues_of_left_homogeneous_patterns"].sel(mode = 2).pvalues_of_left_homogeneous_patterns

draw_data.plot.contourf(
    ax = axi, levels = 21,
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
ecl.plot.draw_significant_area_contourf(p_data, ax = axi, thresh=0.1, transform=proj_trans)

axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('Left Homogeneous Patterns')

# ---------------
axi = ax[1, 1]

draw_data = mca_analysis_result["homogeneous_patterns/right_homogeneous_patterns"].sel(mode = 2).right_homogeneous_patterns
p_data = mca_analysis_result["homogeneous_patterns/pvalues_of_right_homogeneous_patterns"].sel(mode = 2).pvalues_of_right_homogeneous_patterns

draw_data.plot.contourf(
    ax = axi, levels = 21,
    vmax = 0.8, vmin = -0.8,
    cmap = "RdBu_r",
    transform = proj_trans,
    cbar_kwargs={"location": "bottom", "aspect": 50, "pad" : 0.1}
)
ecl.plot.draw_significant_area_contourf(p_data, ax = axi, thresh=0.1, transform=proj_trans)

axi.coastlines()
axi.gridlines(draw_labels=["left", "bottom"], color="grey", alpha=0.5, linestyle="--")
axi.set_title('Right Homogeneous Patterns')
Left Heterogeneous Patterns, Right Heterogeneous Patterns, Left Homogeneous Patterns, Right Homogeneous Patterns
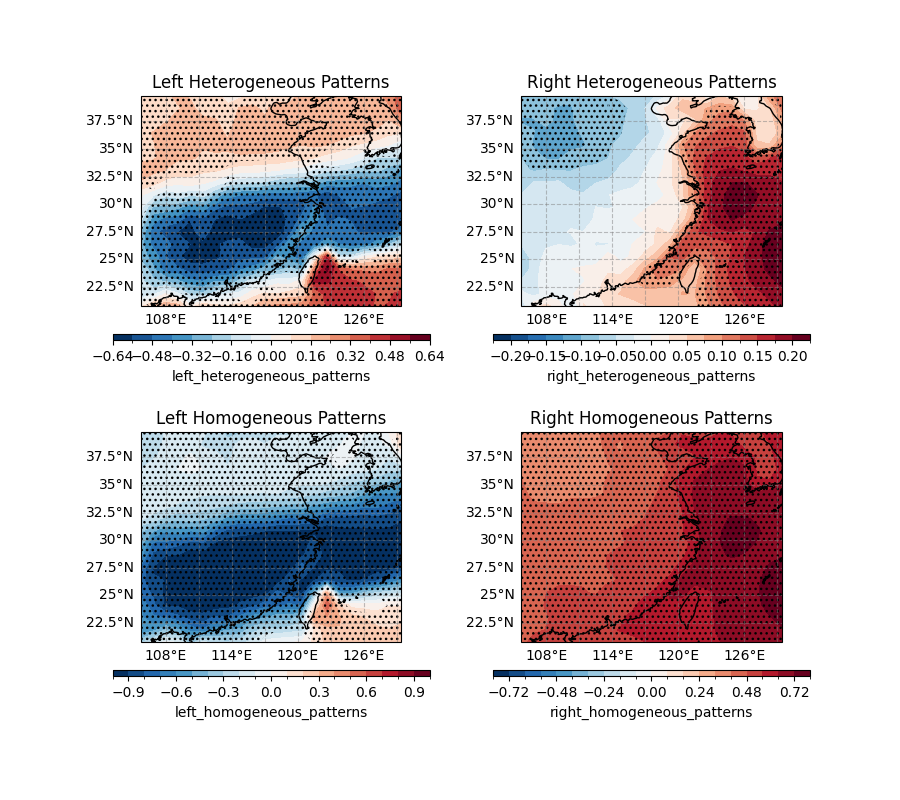
Text(0.5, 1.0, 'Right Homogeneous Patterns')

Total running time of the script: (0 minutes 7.133 seconds)

Contents