Taylor Diagram#

The Taylor Diagram is a graphical tool introduced by American meteorologist Karl E. Taylor in 2001 to assess the performance of models. It provides an intuitive way to compare how well model simulations match observed data and to compare the performance of different models.

The basic structure of the Taylor Diagram includes radial and tangential coordinates. In the chart, the standard deviation of observed data is placed at the center, while the standard deviation of model simulations extends radially outward. Additionally, the correlation coefficient, which measures the strength and direction of the linear relationship between two sets of data, is represented along the tangential axis. This chart allows for a visual comparison of the dispersion, shape, and correlation with observed data.

The advantages of the Taylor Diagram in research, particularly in comparing climate model simulation performance, are as follows:

Intuitiveness: The Taylor Diagram presents the similarity between model simulations and observed data in an intuitive way, making it easy for researchers, including non-experts, to quickly understand model performance.
Comprehensive Comparison: The Taylor Diagram allows for the simultaneous comparison of model simulations with observed data and the performance of multiple models. This aids in identifying the most accurate models.
Comprehensive Assessment: By combining key statistical measures such as standard deviation and correlation coefficient, the Taylor Diagram offers a comprehensive evaluation of model performance, considering multiple aspects rather than focusing on a single parameter.
Wide Applicability: The Taylor Diagram is not limited to climate model performance; it can be applied to evaluate models in various fields such as meteorology, oceanography, and environmental science.

The Taylor Diagram, as a graphical tool, provides a clear and comprehensive way for researchers, including those without a specialized background, to assess model performance. It is particularly useful for comparing multiple models and complex datasets in research.

Build Dataset#

easyclimate.plot.calc_TaylorDiagrams_metadata provides us with the necessary parameters for calculating the subsequent Taylor diagram.

taylordiagrams_metadata = ecl.plot.calc_TaylorDiagrams_metadata(
    f=[da_a, da_b],
    r=[da_obs, da_obs],
    models_name=["f1", "f2"],
    weighted=True,
    normalized=True,
)
print(taylordiagrams_metadata)

  item       std        cc  centeredRMS       TSS
Obs  1.000000  1.000000     0.000000  1.002003
 f1  0.404621 -0.429398     1.229311  0.003210
 f2  2.056470  0.984086     1.087006  0.600409

Basic Figure Framework#

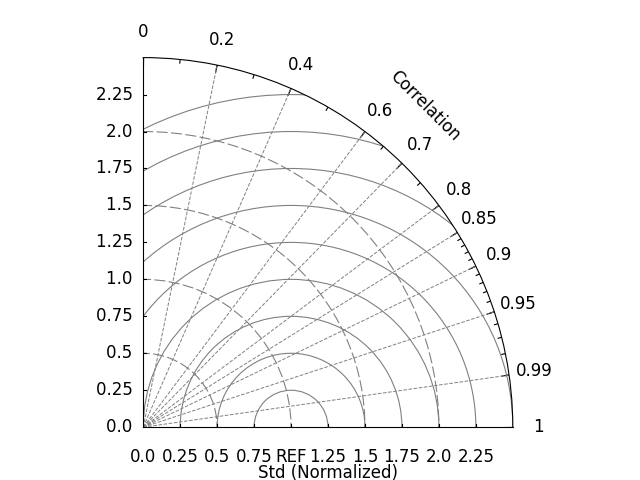
easyclimate.plot.draw_TaylorDiagrams_base can draw the basic framework of the Taylor diagram, which provides a basic drawing board for the data we will place.

fig, ax = plt.subplots(subplot_kw={"projection": "polar"})

ecl.plot.draw_TaylorDiagrams_base(ax=ax, std_max=2.5)

Dataset Points#

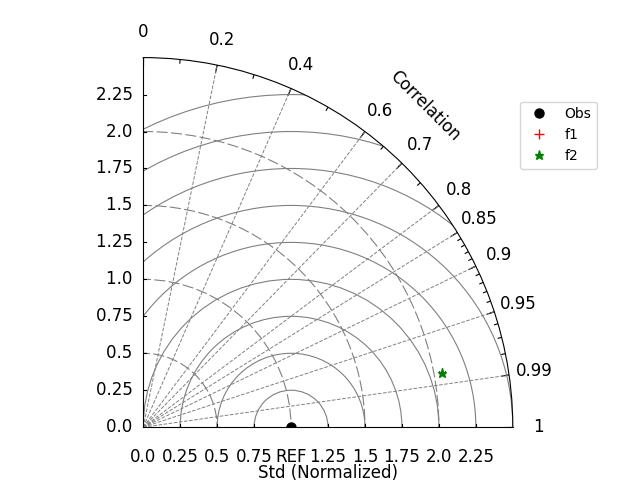
Try using easyclimate.plot.draw_TaylorDiagrams_metadata to place data on the basic framework of the Taylor diagram.

Note

ax.legend() or plt.legend() can add legend for Taylor diagram.

fig, ax = plt.subplots(subplot_kw={"projection": "polar"})

ecl.plot.draw_TaylorDiagrams_base(ax=ax, std_max=2.5)

ecl.plot.draw_TaylorDiagrams_metadata(
    taylordiagrams_metadata,
    ax=ax,
    marker_list=["o", "+", "*"],
    color_list=["black", "red", "green"],
    label_list=["", "", ""],
    legend_list=taylordiagrams_metadata["item"].to_list(),
    cc="cc",
    std="std",
)

ax.legend(bbox_to_anchor=(1, 0.9))

<matplotlib.legend.Legend object at 0x7f804de3bc70>

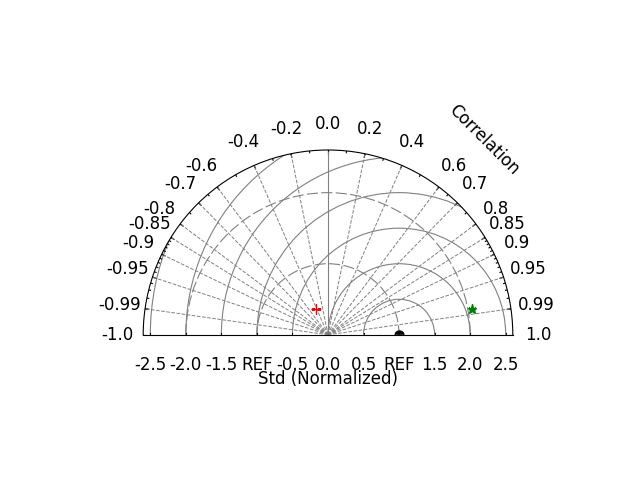
The parameter half_circle = True in easyclimate.plot.draw_TaylorDiagrams_base can make the entire Taylor drawing board appear in a semi circular state, which allows us to discover data points with negative standardized standard deviation (marked with a red cross)

fig, ax = plt.subplots(subplot_kw={"projection": "polar"})

ecl.plot.draw_TaylorDiagrams_base(
    ax=ax,
    std_max=2.6,
    std_interval=0.5,
    half_circle=True,
    x_label_pad=0.5,
    arc_label_pad=0.5,
)

ecl.plot.draw_TaylorDiagrams_metadata(
    taylordiagrams_metadata,
    ax=ax,
    marker_list=["o", "+", "*"],
    color_list=["black", "red", "green"],
    label_list=["", "", ""],
    legend_list=taylordiagrams_metadata["item"].to_list(),
    cc="cc",
    std="std",
)

[<matplotlib.lines.Line2D object at 0x7f804e191ed0>, <matplotlib.lines.Line2D object at 0x7f804e192320>, <matplotlib.lines.Line2D object at 0x7f804dfdc070>]

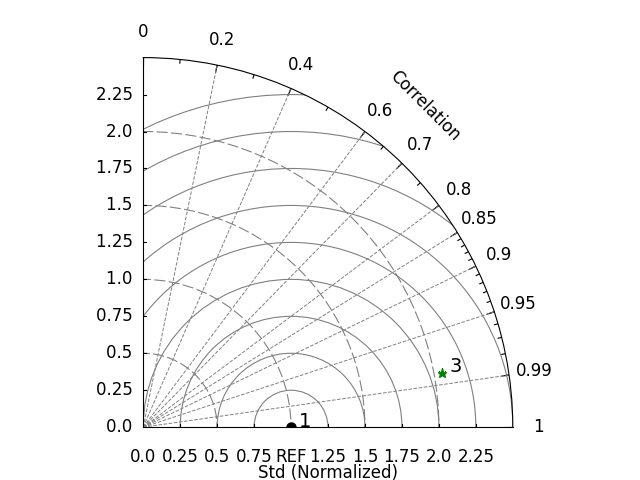
Points’ Labels#

label_list in easyclimate.plot.draw_TaylorDiagrams_metadata can specify the labels of these data points

fig, ax = plt.subplots(subplot_kw={"projection": "polar"})

ecl.plot.draw_TaylorDiagrams_base(ax=ax, std_max=2.5)

ecl.plot.draw_TaylorDiagrams_metadata(
    taylordiagrams_metadata,
    ax=ax,
    marker_list=["o", "+", "*"],
    color_list=["black", "red", "green"],
    label_list=["1", "", "3"],
    legend_list=taylordiagrams_metadata["item"].to_list(),
    cc="cc",
    std="std",
)

[<matplotlib.lines.Line2D object at 0x7f804de7b280>, <matplotlib.lines.Line2D object at 0x7f804de7b700>, <matplotlib.lines.Line2D object at 0x7f804de7b100>]

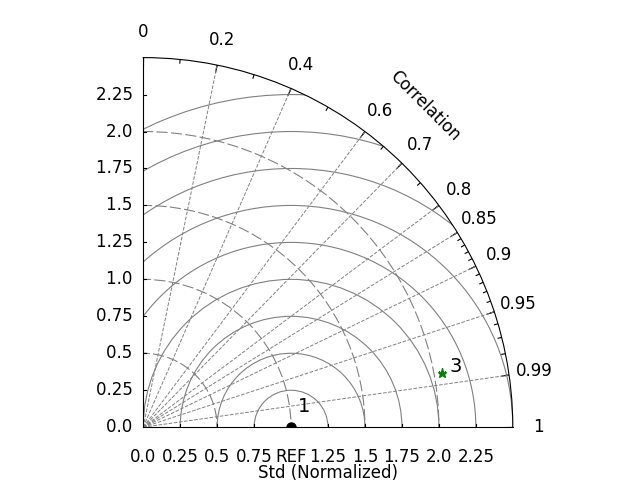
The position of these labels can be finely adjusted using point_label_yoffset and point_label_xoffset.

fig, ax = plt.subplots(subplot_kw={"projection": "polar"})

ecl.plot.draw_TaylorDiagrams_base(ax=ax, std_max=2.5)

ecl.plot.draw_TaylorDiagrams_metadata(
    taylordiagrams_metadata,
    ax=ax,
    marker_list=["o", "+", "*"],
    color_list=["black", "red", "green"],
    label_list=["1", "", "3"],
    legend_list=taylordiagrams_metadata["item"].to_list(),
    cc="cc",
    std="std",
    point_label_yoffset=[0.05, 0, 0.05],
    point_label_xoffset=[0.1, 0, 0],
)

[<matplotlib.lines.Line2D object at 0x7f804dd3a5f0>, <matplotlib.lines.Line2D object at 0x7f804dd3b3a0>, <matplotlib.lines.Line2D object at 0x7f804dd3bb80>]

Total running time of the script: (0 minutes 2.640 seconds)